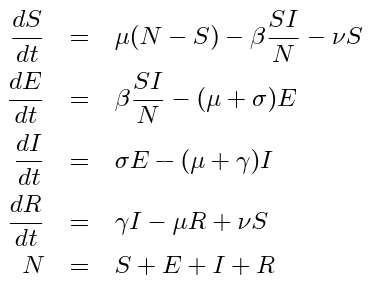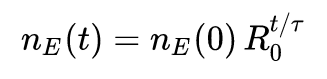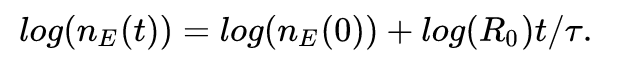Category: ONA

Slajdy do wykładu można znaleźć tu: ONA1-Arytmetyka

Kiedy tylko LabKom uruchomi dla nas kursy w moodle’u, przeniesiemy się tam z materiałami do tego przedmiotu. Będę Państwa informował o tym e-mailem.

Pracujemy w narzędziu python3 (nie w octave) i wykonujemy zadania częściowo inspirowane zadaniami z labu 3 do metod numerycznych. Zachęcam do użycia interpretera ipython3, jeśli pracują Państwo na domowym komputerze. Jeśli ktoś ma kłopoty z interpreterem w domu, to może korzystać z serwera jupyter, używając hasła  podanego na wykładzie. Proszę wtedy pracować w osobnych podpisanych  notebookach. Nieco więcej technicznych/matematycznych szczegółów jest też dostępne w materiałach do wykładu z metod numerycznych.

Będziemy też korzystać z modułu numpy (pisząc “import numpy as np”)  a w szczególności z jego typów danych float64 i float128

Uwaga nt. liczb całkowitych. Obecnie python3 ukrywa zupełnie przed nami fakt istnienia ograniczeń wielkości rejestrów przy operacjach na liczbach całkowitych. Aby zobaczyć jak to działa, warto uruchomić interpreter python2.7 i wykonać operacje na dużych liczbach.

 

W szczególności:

1. Policz epsilon maszynowy (zarówno jako wartość dziesiętną ale też liczbe bitów cechy binarnej przy pomocy sprawdzania dla jakich n 1.0+2.0**(-n) >1.0. Co by się stało, gdybyśmy wykonali tę próbę w okolicy 0.0 zamiast 1.0. Czy taki epsilon maszynowy zależy od liczby bitów cechy, czy mantysy?

2. Oblicz wartość funkcji (pochodzącej od Siegfrieda Rump’a): f(x,y)= 333.75*y**6+x**2*(11*x**2*y**2-y**6-121*y**4-2)+5.5*y**8+x/(y*2) w punkcie x=77617, y=33096. Wykonaj obliczenia w pythonie2, pythonie3, np.float64, np.float32, np.float128 i module Fractions. Jakie błędy obliczeń tam zachodzą? Jeśli ktoś napisze program obliczający tę wartość prawidłowo, i prześle mi przez moodle program i prawidłowy wynik, to dostanie dodatkowy (bonusowy) punkt do zaliczenia.

3(*). Zastanów się nad zadaniem z szeregami zbieżnymi (lub rozbieżnymi) numerycznie ( w materiałach do labu 3). Zaimplementuj liczenie sum S(n) w pythonie, dla dowolnego n i dla kilku szeregów podanych w rozwiązaniu. Które z nich można dokładnie policzyć pry użyciu modułu Fractions?

4(*). Policz wartości e(x) wg rozwinięcia wzoru Taylora dla zadanego maksymalnego stopnia. Porównaj różnicę wyniku jaki otrzymujesz dla x=-90 i x=2.

5(*). Policz sumy częściowe szeregu harmonicznego przy użyciu liczb zmiennoprzecinkowych i przy użyciu modułu Fractions. Porównaj wyniki.

 

W naszym ostatnim i zarazem największym zadaniu zaliczeniowym odejdziemy od tematyki epidemiologicznej i zajmiemy się przetwarzaniem obrazów i ich kompresją. Konkretnie, naszym zadaniem będzie napisanie programu pozwalającego na “ukrywanie” informacji w obrazach, czyli steganografię. Wykorzystamy najprostszą metodę steganografii, czyli wykorzystanie modyfikacji najmniej znaczącego bitu do zakodowania “ukrytej informacji”.

Zasada działania:

Załóżmy, że mamy do przekazania komuś wektor bitów S, długości N  (może to być obraz, lub tekst – jest to dla nas w tej chwili bez znaczenia). Możemy wziąć jakiś obraz reprezentowany w standardowym formacie RGB, z 8 bitami na kanał i powiedzmy wymiarach 2000×1000 pikseli. Obraz ten, możemy wczytać do pamięci w postaci macierzy M o wymiarach 2000x1000x3 z typem danych int8uint8. Zauważmy, że każda z liczb w tej macierzy zawiera intensywność jednego z kolorów podstawowych w  postaci wartości od 0 do 255. Niewielkie zmiany tych wartości (np. o 1) nie są łatwo postrzegalne dla ludzkich oczu, ale program komputerowy może bardzo łatwo je wykryć.

Nasze zadanie będzie polegało na tym, że każdy kolejny bit z wektora S “wstawiać” jako ostatni bit kolejnego bajtu macierzy M. Jak go wstawiać? otóż wystarczy, że sprawdzimy czy reszta z dzielenia kolejnego bajtu macierzy M przez 2 jest równa wartości odpowiedniego bitu z wektora S.

M.reshape((2000*1000*3,))[i]%2 == S[i]

Jeśli tak, to nic nie musimy robić. Jeśli nie, to musimy odjąć lub dodać 1 do M.reshape((2000*1000*3,))[i], żeby nasze równanie było prawdziwe (uważając przy tym aby nie odjąć od zera ani nie dodawać do 255).

W ten sposób otrzymujemy nową macierz M, która ma tę własność, że ostatnie bity reprezentacji kolejnych bajtów M są równe kolejnym bitom S. Taki plik możemy zapisać jako obraz i będzie on bardzo subtelnie wizualnie zmieniony, natomiast odbiorca tego pliku, który wie czego szukać może bardzo łatwo odczytać wektor S

Aby rozwiązanie było praktyczne, musimy jeszcze być w stanie podać długość wektora S oraz typ danych do zapisu tego wektora. W naszym rozwiązaniu, pierwszy zakodowany bit (M[0]%2) będzie określał, czy mamy do czynienia z tekstem w alfabecie DNA (M[0]%2==0) czy z obrazem w skali szarości (M[0]%2==1). Kolejne 32 bity będą podawać nam długość ciągu DNA (w postaci jednej 32 bitowej całkowitej liczby dodatniej w kodzie dwójkowym) lub wymiary obrazka (w postaci dwóch 16bitowych całkowitych liczb dodatnich oznaczających odpowiednio szerokość x i wysokość y zakodowanego obrazka).

Zadanie: 

Napisz moduł pythonowy (z komentarzami!) o nazwie stegano.py,  który realizuje następujące funkcje:

1. read_image_greyscale (image_file) – zwracający wymiary obrazka oraz ciąg bitów wartości na podstawie pliku w formacie png (2 pkt)
2. write_image_greyscale (x,y,bit_vector,output_image_file) – zapisujący obrazek do formatu png w skali szarości (2pkt)
3. read_DNA(text_file) – zwracający ciąg bitów na podstawie pliku tekstowego zawierającego wyłącznie alfabet ACGT (kodowanie bitowe: A=00 ,C=01, G=10, T=11) (2 pkt)
4. write_DNA(bit_vector,output_text_file) – zapisuje ciąg liter DNA do pliku tekstowego na podstawie ciągu bitów wg powyższego kodowania (2 pkt)
5. encode_DNA(bit_vector,image_file, output_file) – wczytujący obraz RGB z pliku image file i zakodowujący wektor bit_vector reprezentujący DNA w ostatnich bitach obrazu (zgodnie z powyższym opisem, łącznie z 33 bitami nagłówka). Zmodyfikowany obraz powinien być zapisany do pliku output_file. Jeśli obraz jest za mały aby zakodować cały wektor, program powinien zwrócić błąd. (5 pkt)
6. encode_image(bit_vector,x,y,image_file,output_file) – wczytujący obraz RGB z pliku image file i zakodowujący wektor bit_vector reprezentujący obraz w ostatnich bitach obrazu (zgodnie z powyższym opisem, łącznie z 33 bitami nagłówka). Zmodyfikowany obraz powinien być zapisany do pliku output_file. Jeśli obraz jest za mały aby zakodować cały wektor, program powinien zwrócić błąd. (5 pkt)
7. decode(image_file, output_file) – powinien wczytywać obraz RGB z pliku, odczytywać z nagłówka (33 ostatnie bity z pierwszych 33 bajtów) informację o tym, czy zakodowane jest DNA, czy obraz, następnie odkodowywać informację i zapisać (korzystając z write_DNA lub write_image_grayscale) wynik do pliku output_file. (5 pkt)
8. main(), która powinna umożliwiać zakodowywanie i odkodowywanie informacji przy pomocy parametrów z linii komend obsługiwanych przy pomocy modułu Argparse. (2 pkt)

Terminy:

Rozwiązania (w postaci e-maila z normalnym załącznikami w postaci pliku stegano.py  oraz zakodowanych przykładowych danych i dopiskiem [ONA-3] w temacie) w ciągu 3 tygodni od dzisiaj, czyli do 18. VI 2020

Przykładowe dane:

Można popróbować np. zakodować taki obrazek:

lub kod DNA koronawirusa covid-19.fasta

W jakimś ulubionym pliku ze zdjęciem przedstawiającym swoją fizjonomię.

Wersja bonusowa (+5 pkt)

Można wyposażyć nasz program w dodatkową funkcjonalność polegającą na kompresji ciągu bitów przed zakodowaniem. Jeśli ktoś zaimplementuje kompresję (i dekompresję) metodą LZ77 to może otrzymać dodatkowe 5 punktów).

Dziś przede wszystkim zajmowaliśmy się zerami funkcji nieliniowych, ale zrobiliśmy też dygresję (w zasadzie uzupełnienie do wykładu o całkowaniu numerycznym) n.t. metod Monte Carlo. Notatki do równań nieliniowych znajdą Państwo tu. Opis całkowania metodą MC znajdą Państwo np. tu

Zadania na dziś:

1. Napisz program, który znajduje  przybliżenie liczby Pi przy pomocy równania x**2+y**2<=1

2. Napisz program, który korzysta z metody bisekcji i oblicza wartość pierwiastka kwadratowego z 2. Jakiego równania zera szukamy? ile iteracji potrzeba?

3. Napisz program, który korzysta z metody stycznych, aby obliczyć tę samą wartość. O ile szybciej możemy znaleźć dokładną wartość?

4 (*). Zaimplementuj metodę iteracji prostej Banacha dla rozwiązania równania Keplera.  Możesz posiłkować się tym artykułem

Materiały do powtórki przed kolokwium: ONA_powtorka

Kwestie organizacyjne – Na ostatnim wykładzie za dwa tygodnie  (4. czerwca) będziemy mieli kolokwium (przeprowadzone online, podczas wykładu). Będzie to test, podobny do wcześniejszych: kolokwium-2017, z tym, że przeprowadzony przy pomocy systemu online. Podobnie zrobimy z egzaminem, w czasie sesji.

Ostatnie, trzecie, zadanie zaliczeniowe opublikuję dopiero za tydzień, ale będą Państwo mieli nadal 3 tygodnie na wykonanie go, czyli do 18. czerwca.

Dzisiejszy wykład porównujący cechy różnych pakietów do obliczeń jest tu: ONA12-Obliczenia-symboliczne-i-pakiety

Zadania na dziś są dość proste i dotyczą przede wszystkim obliczeń symbolicznych i pakietu sympy (można to robić w platformie jupyter)

1. Przy użyciu pakietu sympy, zbadaj podstawowe możliwości obliczeń symbolicznych: stwórz zmienną sumboliczną x (Symbol(‘x’)), stwórz wyrażenie wielomianowe (np. x**2-2) oraz wyrażenie trygonometryczne (np. sin(x)) i policz dla nich pochodne, całki (oznaczone i nieoznaczone) oraz granice (w 0, z prawej i lewej strony oraz , granice 1/x w nieskonczonosci: sympy.oo,).
2. Zobacz jak wyniki tego typu zadań wyglądają w Wolfram Alpha
3. Zarejestruj się w systemie SageMath i tam spróbuj rozwiązać te same problemy
4. (*) Spróbuj rozwiązać symbolicznie układ równań różniczkowych zwyczajnych z poprzednich zajęć (model Lotki-Volterry albo Zombie Invasion) w jednym z wymienionych wcześniej pakietów

Dziś będziemy zajmować się różniczkowaniem i całkowaniem numerycznym. Slajdy są tu: ONA11-calkowanie ONA11-calkowanie

Przydatny będzie nam przede wszystkim pakiet scipy.integrate ale będziemy też korzystać z nowych funkcji pakietu matplotlib, takich jak wykresy strzałkowe

0. Na początek proponuje obejrzeć sobie program opisujący model Lotki-Volterry ( lotka_volterra ) i spróbować wykonać go po kawałku ze zrozumieniem. Jeśli są pytania, to proszę pytać

1. Naszym głównym zadaniem zwykle było zadanie o zombie (tutaj wersja zeszłoroczna). W związku z okolicznościami przyrody, może lepiej zajmiemy się modelem SEIR ewolucji epidemii. Jest to model opisany równaniami:

Gdzie:

• S to liczba osób niezarażonych,
• E to liczba osób zarażonych, ale jeszcze nie zarażających,
• I to liczba osób zarażonych i zarażających
• R to liczba osób, które już ozdrowiały i nie są podatne na zarażenie

Model ma następujące parametry:

• \beta to współczynnik “skuteczności zarażania”
• \sigma to współczynnik “inkubacji” im większy, tym krótsza inkubacja
• \gamma to współczynnik “zdrowienia” im większy, tym krótszy czas “zarażania”
• \nu to współczynnik “zyskiwania/utraty odporności”, jeśli jest dodatni, część populacji zyskuje odporność bez chorowania, jeśli jest ujemny, część populacji traci odporność po ozdrowieniu
• \mu to współczynnik normujący związany ze śmiertelnością populacji. Ten model zakłada stałe N w czasie, ale zawiera przepływy normujące \mu, które związane są z efektami śmiertelności na populacje

Interesują nas następujące pytania:

a) Jak wygląda ewolucja systemu w czasie (w zakresie 0..50),  jeśli na początku jest tylko 1000 ludzi niezarażonych, i jeden zarażony  i mamy następujące prametry:

• \beta=0.9
• \gamma=0.2
• \sigma=0.5
• \mu=0
• \nu=0

Rozwiązanie przedstaw na wykresie 4 zmiennych (S, E, I, R) od czasu

b) Jak na sytuację wpłyną zmiany współczynnika \nu? Co jeśli \nu jest ujemne, jak w przypadku grypy? Co jeśli \nu jest dodatnie, co oznaczałoby spontaniczne zyskiwanie odporności, bez fazy zarażania?

c) Zaprezentuj pole wektorowe populacji S i I względem parametrów \beta i \gamma?

d*) Zaprezentuj pole wektorowe 3d dla zmiennych SEI

Praca domowa (za 1 pkt)

Trzeba zaimplementować model z niezerową śmiertelnością (powiedzmy \mu=0.01), wykonać symulacje i opisać jednym zdaniem co się zmienia jeśli chodzi o liczbę chorych infekujących (I) w stosunku modelu z \mu=0.

Żeby dostać ten punkt, trzeba wysłać do mnie jako załącznik plik .py generujący wykresy (SEIR od czasu) dla dwóch modeli (\mu=0 i \mu=0.01) a w treści wiadomości napisać co zaobserwowaliśmy. Czas, jak zwykle, do następnych zajęć.

Dziś poznaliśmy numeryczne rozwiązania problemu znajdowania dominujacych wartości własnych metodą potęgową i wartości własnych bliskich zadanej wartości metodą odwrotną potęgową. Dużo więcej materiału można znaleźć na tej stronie

Jeśli chodzi o funkcje przydatne w pythonie, to przede wszystkim interesują nas funkcje:

scipy.linalg.eig(A)

oraz

scipy.linalg.eigvals(A)

Zadania na dziś:

1. Zaimplementuj metodę potęgową z wykładu i zastosuj ją dla rozważanej na wykładzie macierzy: M=array([[1,2.],[4,3]]). Czy Twoje rozwiązanie różni się od rozwiązania z funkcji eig? Jakie równanie spełniają wektory własne zwrócone przez tę funkcję i Twoją metodę?

2. Zaimplementuj metodę Rayleigha RQI (z wykładu ). zastosuje ją do znalezienia najmniejszej wartości własnej macierzy M z zad. 1.

3. Rozważ macierz A=array([[-1,2,2],[2,2,-1.],[2,-1,2]]). Spróbuj znaleźć jej wartości własne zaimplementowanymi przez siebie metodami. Skąd biorą się problemy? Czy podobne problemy spotkają nas dla macierzy rand(3,3)?

4. Rozważ macierz M=array([[a,1.],[0,b]]). Gdzie a i b są dodatnimi liczbami całkowitymi. Jak zmienią się wartości własne, gdy zamiast zera wstawimy do M[1,0] wartośći 1/k dla k rosnącego wykładniczo?

Naszym zadaniem będzie implementacja funkcji, która będzie wykorzystywac metodę liniowych najmniejszych kwadratów, aby znaleźć podstawową liczbę odtwarzania dla przypadków COVID-19 w Polsce.

W naszym (niezmiernie uproszczonym i nie nadającym się do zastosowań praktycznych, ale ilustrującym kluczowe idee) modelu, przyjmiemy, że początkowy rozwój wirusa w populacji rośnie wg wykładniczego wzrostu:

gdzie t oznacza czas (w dniach), n_E(t) oznacza liczbę osób chorych w momencie t, R_0 jest szukaną podstawową liczbą odtwarzania, zaś \tau przyjmiemy za równą 1.

Nasz program będzie wykorzystywał fakt, że to równanie po obustronnym zlogarytmowaniu staje się liniowe:

Jeśli mamy dane o liczbie potwierdzonych chorych w pewnym okresie (dla każdego kolejnego dnia), znamy \tau, to możemy wykorzystać liniową ważoną metodę najmniejszych kwadratów do dopasowania rozwiązania, aby znaleźć log(R_0).

Warto  pamiętać, że w tym przypadku, jeśli nie zastosujemy wag w metodzie najmniejszych kwadratów, nasza metoda będzie minimalizować |log(x)-log(b)|^2, co nie będzie prawidłowe. Jak widać na poniższym rysunku, dopasowanie do danych jest lepsze (zwłaszcza z prawej strony) dla problemu ważonego.

Dlatego warto przypomnieć sobie zadanie o ważonym zagadnieniu liniowych największych kwadratów, które ma podane rozwiązanie w materiałach do metod numerycznych. W naszym przypadku wagi w_i są równe n_E(i).

Punktacja:

1. Napisanie funkcji wykorzystującej funkcję scipy.linalg.lstsq (proszę nie używać funkcji typu polyfit) i obliczającej ważony liniowy problem najmniejszych kwadratów (5 pktów)
2. Napisanie funkcji wykorzystującej funkcję urlopen() i dane dostępne publicznie aby pobrać pierwsze 28 dni, kiedy w wybranym kraju (np. Polsce) występowały zachorowania (tj. pomijając pierwsze zera w linii odpowiadającej danemu krajowi) (5 pktów)
3. Napisanie programu, który wykorzystuje te dane, aby obliczyć R_0 zgodnie z wzorami podanymi powyżej. Program powinien też generować wykres podobny do powyższego. (5 pktów)

Rozwiązania należy nadsyłać w ciągu dwóch tygodni (czyli do 13. maja włącznie) na mój adres e-mail z dopiskiem [ONA-2] w tytule. Jak zwykle, proszę o skomentowane pliki .py jako normalne załączniki.

Tym razem zajmiemy się Interpolacją funkcji przy pomocy wielomianów i funkcji sklejanych.

Teoria z wykładu jeśli chodzi o wielomiany znajduje się tu a jeśli chodzi o funkcje sklejane tu.

Większość interesujących nas dzisiaj funkcji znajdziemy w module scipy.interpolate, ale najprostsze funkcje polyfit  i poly1d znajdują się w module numpy.  W module interpolate interesują nas funkcje:

• InterpolatedUnivariateSpline
• UnivariateSpline
• lagrange

Na laboratorium będziemy rozwiązywać następujące problemy:

1. Spróbuj zinterpolować funkcję sinus(x) na przedziale [0,math.pi] korzystając z równoodległych N węzłów (np. wygenerowanych używając np.linspace(0,math.pi,N)). Jak zachowuje się błąd średniokwadratowy tej interpolacji dla punktów np.linspace(0.math.pi,1000), gdy N rośnie?

2. korzystając z przykładu pokazanego na wykładzie, gdzie wartości y_i=[1,1,1,2], czy potrafisz dobrać pozycje x_i=[1,x2,x3,4] tak aby uzyskać dowolnie dużą amplitudę interpolowanego (polyfit(x_i,y_i,s=0) wielomianu na przedziale [1,4]? Czy błąd aproksymacji (polyfit, k=2) wielomianem stopnia 2 jest tak samo duży?

3. Spróbuj interpolować te same dane przy pomocy krzywych sklejanych. Czym różnią się splajny dla różnych k (k=1,2,3)?

4. Wygeneruj zaburzone obserwacje wg funkcji y=log_2(x) + scipy.stats.normal() w wielu (~1000) punktach na przedziale 1..100. Czy lepiej będzie interpolować, czy aproksymować aby znaleźć kształt funkcji?

 

Dzisiaj na wykładzie omówiliśmy zasadniczo tematy zawarte w wykładzie 12. z metod numerycznych. Jeśli ktoś chciałby doczytać to znajdzie materiały tutaj

Zadania na lab:

0. Rozważmy cztery punkty na płaszczyźnie: (0,4), (1,0), (2,0) i (3,0). Jaka prosta przechodzi najbliżej nich? ułóż układ równań liniowych, który można rozwiązać metodą najmniejszych kwadratów. Wykorzystaj funkcje scipy.linalg.qr aby zobaczyć rozkład QR macierzy A. Użyj funkcji scipy. linalg.lstsq aby znaleźć rozwiązanie. Jakie jest znaczenie wartośći zwróconych przez tę funkcje?

1. Rozważmy dane:

x	f(x)
0.00	4.00000000000000e+00
1.25	3.28650479686019e+00
2.50	3.08208499862390e+00
3.75	3.02351774585601e+00
5.00	3.00673794699909e+00
6.25	3.00193045413623e+00
7.50	0.00055308437015e+00
8.75	3.00015846132512e+00
10.00	3.00004539992976e+00

Jak będzie wyglądało dopasowanie met. najlepszych kwadratów funkcji f(x)=a*1+b*exp(-x) do tych danych?

2. Rozważmy dane o obwodzie pnia, trees-stripped ( do wczytywania przyda się funkcja numpy.loadtext). Kolejne kolumny oznaczają tu:

• obwód pnia
• wysokość drzewa
• objętość pozyskanego drewna.

Spróbuj dopasować (metodą najmniejszych kwadratów) objętość drzewa jako funkcję:

• kombinację liniową obwodu pnia i wysokości drzewa
• iloczynu wysokości przez obwód
• kombinację liniową powyższych

Gdzie uzyskujemy najmniejszy błąd przybliżenia?

3(*). Przedstaw na wykresie wynik zadania 1 (wykres punktowy obserwacji i dużo gęściej próbkowany wykres liniowy znalezionej funkcji). Jaki jest problem naszego rozwiązania? czy można jakoś pomóc sobie używając ważonego problemu średnich kwadratów? jak to zrobić dla wagi jednej z obserwacji=0? a jak dla wagi 0.1?

 

Dziś zajmujemy się układami równań liniowych w reprezentacji macierzowej.

Wykład będzie prowadzony prz tablicy, więc slajdów nie ma, ale potrzebne materiały ( i dużo więcej niż nam potrzeba) są dostępne w materiałach do wykładu z Metod numerycznych . Nas w szczególności interesują wykłady 5 (eliminacja Gaussa) i 7 (uwarunkowanie problemu). Można też zajrzeć do wykładu 8 (macierze rzadkie), ale jest on o dla nas zdecydowanie zbyt obszerny, a  dla nas to tylko temat poboczny.

Jeśli chodzi o operacje algebry liniowej w pythonie, podczas laboratorium przydadzą nam się następujące biblioteki:

numpy.linalg – podstawowe operacje na macierzach, m.in. cond (A), det(A)

scipy.linalg – nieco więcej operacji na macierzach, m.in. hilbert(N), solve(A,B)

scipy.sparse.linalg – operacje na macierach rzadkich m.in. spsolve(A,B)

scipy.io – wczytywanie różnych ciekawych formatów – np. macierzy rzadkich w formacie matlaba loadmat(f)

Zadania na laboratorium :

1. Stwórz macierz Hilberta H[i,j]=1/i+j-1 dla sensownie dużego rozmiaru macierzy (100×100, 200×200) i wyświetl ją przy pomocy imshow() z biblioteki matplotlib
2. Przypomnij sobie rozwiązywanie ukł. równań poprzez rozkład LU. Zaimplementuj ręcznię tę metodę (w wersji bez wyboru el. głównego) i spróbuj rozwiązać tym sposobem układ postaci A= np.array([[1e-18,1.0],[1.0,2.0]]) B=np.array([1.0,4.0]). Porównaj wynik z wynikiem scipy.linalg.solve(A,B). Dlaczego w przypadku tej macierzy wybór elementu głównego ma takie znaczenie?
3. Korzystając z metody scipy.rand(1000,1000) stwórz macierz losową. Użyj jej do przetestowania rozkładu macierzy  LU (scipy.linalg.lu) w wersji z permutacją i bez. Rozwiąż taki układ (dla b=scipy.rand(1000)) przy pomocy scipy.linalg.solve()
4. Załóżmy, że mamy teraz jedną macierz A (my użyjemy losowej) i bardzo wiele różnych warunków brzegowych B (my wylosujemy 1000). Spróbuj rozwiązać wszystkie układy równań powstałe z przyrównania tej samej macierzy A do wielu różnych wektorów B. Czy można zamiast korzystać wielokrotnie z funkcji solve() coś przyspieszyć? Np. korzystając z funkcji lu()?
5. Duże macierze równań liniowych często powstają w problemach inżynierskich. Pobierz jedną z macierzy z kolekcji układów powstałych przy projektowaniu elementów samolotów Boeing (np. nr 38 ) i spróbuj wczytać ją jako macierz rzadką do ipython’a. Następnie rozwiąż ją dla losowych warunków brzegowych b.