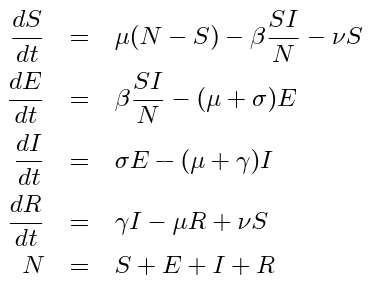Dziś będziemy zajmować się różniczkowaniem i całkowaniem numerycznym. Slajdy są tu: ONA11-calkowanie ONA11-calkowanie
Przydatny będzie nam przede wszystkim pakiet scipy.integrate ale będziemy też korzystać z nowych funkcji pakietu matplotlib, takich jak wykresy strzałkowe
0. Na początek proponuje obejrzeć sobie program opisujący model Lotki-Volterry ( lotka_volterra ) i spróbować wykonać go po kawałku ze zrozumieniem. Jeśli są pytania, to proszę pytać
1. Naszym głównym zadaniem zwykle było zadanie o zombie (tutaj wersja zeszłoroczna). W związku z okolicznościami przyrody, może lepiej zajmiemy się modelem SEIR ewolucji epidemii. Jest to model opisany równaniami:
Gdzie:
- S to liczba osób niezarażonych,
- E to liczba osób zarażonych, ale jeszcze nie zarażających,
- I to liczba osób zarażonych i zarażających
- R to liczba osób, które już ozdrowiały i nie są podatne na zarażenie
Model ma następujące parametry:
- \beta to współczynnik “skuteczności zarażania”
- \sigma to współczynnik “inkubacji” im większy, tym krótsza inkubacja
- \gamma to współczynnik “zdrowienia” im większy, tym krótszy czas “zarażania”
- \nu to współczynnik “zyskiwania/utraty odporności”, jeśli jest dodatni, część populacji zyskuje odporność bez chorowania, jeśli jest ujemny, część populacji traci odporność po ozdrowieniu
- \mu to współczynnik normujący związany ze śmiertelnością populacji. Ten model zakłada stałe N w czasie, ale zawiera przepływy normujące \mu, które związane są z efektami śmiertelności na populacje
Interesują nas następujące pytania:
a) Jak wygląda ewolucja systemu w czasie (w zakresie 0..50), jeśli na początku jest tylko 1000 ludzi niezarażonych, i jeden zarażony i mamy następujące prametry:
- \beta=0.9
- \gamma=0.2
- \sigma=0.5
- \mu=0
- \nu=0
Rozwiązanie przedstaw na wykresie 4 zmiennych (S, E, I, R) od czasu
b) Jak na sytuację wpłyną zmiany współczynnika \nu? Co jeśli \nu jest ujemne, jak w przypadku grypy? Co jeśli \nu jest dodatnie, co oznaczałoby spontaniczne zyskiwanie odporności, bez fazy zarażania?
c) Zaprezentuj pole wektorowe populacji S i I względem parametrów \beta i \gamma?
d*) Zaprezentuj pole wektorowe 3d dla zmiennych SEI
Praca domowa (za 1 pkt)
Trzeba zaimplementować model z niezerową śmiertelnością (powiedzmy \mu=0.01), wykonać symulacje i opisać jednym zdaniem co się zmienia jeśli chodzi o liczbę chorych infekujących (I) w stosunku modelu z \mu=0.
Żeby dostać ten punkt, trzeba wysłać do mnie jako załącznik plik .py generujący wykresy (SEIR od czasu) dla dwóch modeli (\mu=0 i \mu=0.01) a w treści wiadomości napisać co zaobserwowaliśmy. Czas, jak zwykle, do następnych zajęć.