Tym razem nasze zadanie polegać będzie na napisaniu programu, który dla zadanej listy fragmentów białek uzupełnia je do pełnych sekwencji używając programu BLAST, a następnie wyszukuje w tych sekwencjach domen przy pomocy algorytmu HMMER, żeby na koniec sprawdzić istotność wzbogacenia listy białek w konkretne typy domen.
1. (4 pkt) Napisz program extend.py, który dla zadanej listy fragmentów białek w formacie fasta, znajdzie w bazie NCBI (protein non redundant) przy pomocy programu blastp wszystkie sekwencje białkowe o zadanym minimalnym procencie identyczności (domyślnie 90%), i zadanym minimalnym e-value nie większym niż zadana wartość (domyślnie 10e-10) z co najmniej jednym fragmentem z danych wejściowych. Przykładowy plik z danymi: input-z2.fasta. Program powinien przyjmować parametry z linii komend, dokonywać zapytania przez internet, parsować wyjście i zwracać plik .fasta
2. (6 pkt) Napisz program scan_pfam.py, który na podstawie pliku z białkami wykonuje zapytanie do serwera hmmscan (serwer online tu, opis api) i pobiera pliki wynikowe w formacie tsv. Korzystając z plików pobranych z serwera hmmer poda nam w wyniku plik csv, w którym będziemy mieli w wierszach kolejne identyfikatory białek z pliku FASTA, zaś w kolumnach będzie miał kolejne identyfikatory domen białkowych PFAM. Na przecięciu wiersza i kolumny stawiamy 0, jeśli dana domena nie została znaleziona w danym białku, a 1 w przeciwnym wypadku. Warto zorientować się w parserach zawartych w module Bio.SearchIO.HmmerIO. Uwaga: okazuje się, że obecne parsery w tej bibliotece nie obsługują dobrze formatów obecnie zwracanych przez serwer hmmscan. Biorąc pod uwagę, że to bardzo prosty format, z którego potrzebują Państwo tylko kilku kolumn, myślę, że to nie powinno nastręczać kłopotów.
3. (6 pkt ) Napisz program, który dla zadanych dwóch równych plików wynikowych z punktu 2, ( w naszym przykładzie możemy wyliczyć takie pliki dla pliku źródłowego input-z2.fasta i dla pliku wynikowegoz z punktu 1.) wyliczy nam wartość prawdopodobieństwa takiego rozkładu “trafień” przy założeniu, że w obu grupach białek domeny powinny występować równie często. W tym podpunkcie chodzi nam o napisanie implementacji testu Fishera dla naszych danych korzystając z wzoru:
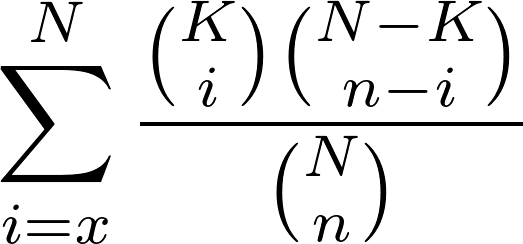, i porównanie wyników do implementacji testu Fishera zaimplementowanego w module Scipy.stats. (Oznaczenia: N – liczba białek w obu plikach, K -liczba białek w pierwszym pliku, n – liczba “trafień” w obu plikach, x – liczba “trafień” w pierwszym pliku).
4. Napisanie raportu dotyczącego dokonanych decyzji implementacyjnych i otrzymanych wyników (domen wzbogaconych w wydłużonych sekwencjach białkowych względem oryginalnych).
Termin na wykonanie zadania to 4 tygodnie (do 18. VI). Rozwiązania przesyłamy mailem na adres bartek@mimuw.edu.pl z dopiskiem [WBO-3-2019] w temacie.
W pierwszym punkcie chodzi rozumiem o maksymalne e-value?
Chodzi o trafienia z e-value nie większym niż zadane. Rzeczywiście zmienię to na maksymalne, żeby nie było wątpliwości.
Co rozumiemy przez ‘liczba “trafień”‘? Jest to równoznaczne z ilością 1 w pliku, czy ilością białek dla których znaleźliśmy co najmniej 1 domenę?
Testy robimy, dla każdej rodziny osobno. liczba trafien jest liczbą jedynek w każdym pliku.
Czy w 1 części zadania mamy uzywać blastp do wyszukiwania całych sekwencji, czy chodzi może tylko o części sekwencji które dają match o zadanych parametrach?
Pytam ponieważ domyślnie blastp nie zwraca takiej informacji z bazy, każdy match zawiera za to część sekwencji dającej dobre lokalne uliniowienie – pytanie czy chodzi o nią, czy też musimy wyszukiwać pełną sekwencję z której taki match pochodzi?
całych sekwencji
Rozumiem, że liczymy sumę pvalue (otrzymanych z użyciem testu Fishera) od ilości trafień w pierwszym pliku, do ilości wszystkich białek w obu plikach (co może wydać się kłopotliwe, gdyż symbol Newtona zakładał liczby >=0, a iterując do N, dochodzimy do liczb ujemnych). Jaka jest właściwie tego idea?
Otrzymane wyniki mamy porównywać do wyników testu Fishera zaimplementowanego w scipy.stats, tam również mamy policzyć taką sumę i to otrzymane sumy porównywać?
liczymy p-value, które jest sumą prawdopodobieństw z rozkładu hipergeometrycznego. Idea tego testu jest dość dobrze znana od niemal stu lat (https://en.wikipedia.org/wiki/Fisher%27s_exact_test). W przypadku, kiedy w naszym wzorze i jest większe niż n lub k, to oczywiście prawdopodobieństwo jest równe 0.