Zadanie zaliczeniowe nr 2 – fraktale

Nasze zadanie polega na napisaniu programu rysującego fraktale w module turtle pythona według reguł opisanych przez nieco uproszczone systemy funkcji iterowanych.

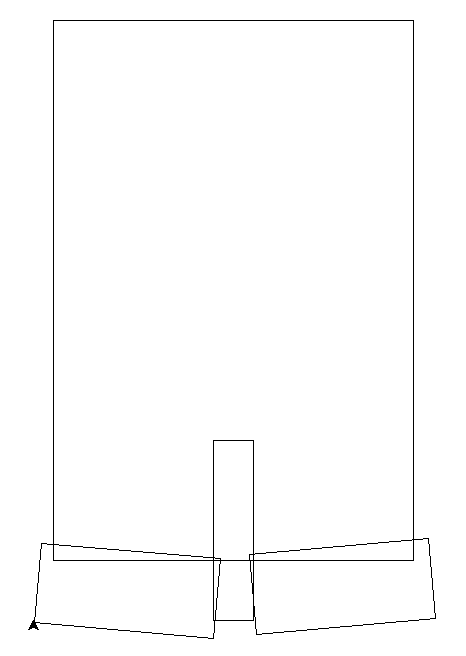
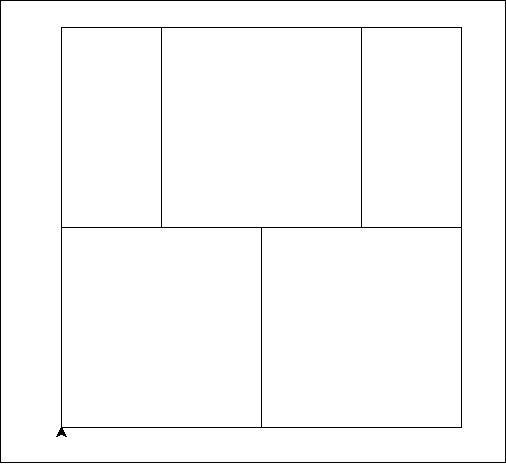
Taki układ funkcji iterowanych będziemy reprezentować jako zestaw prostokątów: prostokąt referencyjny o podanych wymiarach i zestaw prostokątów mniejszych odpowiadających odwzorowaniom zwężającym tegoż prostokąta referencyjnego. Te prostokąty reprezentują samopodobieństwo wyjściowego fraktala. Np. fraktalna choinka (inspirowana nieco paprotką Barnsley’a), może być reprezentowana jako odwzorowanie referencyjnego prostokąta na cztery mniejsze (lewą dolną gałąż, prawą dolną gałąź, “pieniek” i “resztę choinki”) tak jak na rysunkach poniżej:

Rys 1. Prostokąt referencyjny i cztery prostokąty reprezentujące odwzorowania zwężające.

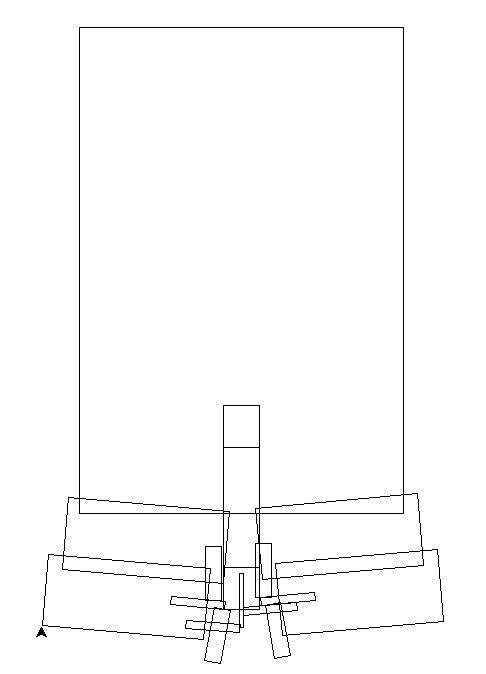
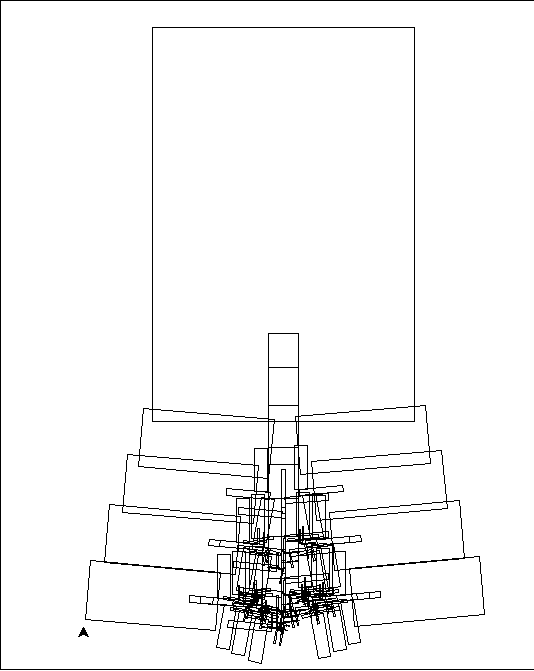
Ponieważ nasz fraktal jest samopodobny, ten proces możemy powtarzać rekurencyjnie, zastępując każdy z tych prostokątów czterema mniejszymi wg tego samego wzoru:

Rys 2. IFS-choinka poziomu2 i poziomu 4.

Niestety koszt rysowania takiej choinki rośnie wykładniczo wraz z głębokością zejść rekurencyjnych, dlatego nie jest to praktyczny sposób rysowania choinek. Z  pomocą przychodzi nam twierdzenie Banacha, które pozwala nam na tworzenie obrazków reprezentujących nasz fraktal (dokładniej: punkt stały układu funkcji iterowanych) przy pomocy losowej iteracji – tzw. gra w chaos.

Taki algorytm działa w następujący sposób: zaczynamy od losowego punktu należącego do naszego prostokąta referencyjnego. Nazwijmy jego współrzędne X, Y. Musimy też wybrać liczbę N, która będzie oznaczać ile punktów z naszego atraktora pojawi się na ekranie. Wykonujemy kolejne kroki wg takiego schematu:

i=0
dopóki i<N:
wybierz losowo jedno z przekształceń zwężających F
oblicz współrzędne X_n,Y_n, które odpowiadają wsp. X,Y po przekształceniu F
narysuj punkt X_n,Y_n
X,Y=X_n,Y_n
i+=1


Uwaga, należy pamiętać, aby podczas losowego wyboru przekształcenia wybierać je proporcjonalnie do pola prostokąta odpowiadającego temu przekształceniu.

Taka procedura prowadzi do dużo milszych dla oka wyników. Np. nasza choinka będzie wyglądać następująco, zależnie od tego, czy narysujemy 1000, czy 10000 o punktów.

Podobnie możemy reprezentować Trójkąt Sierpińskiego jako IFS składający się z 3 przekształceń:

Symulacje takiego prostego IFS dają następujące wyniki (odpowiednio dla 100, 500, 1000 i 3000 punktów):

 

Nasze zadanie zaliczeniowe polega na napisaniu programu, który pozwala na wczytywanie układu IFS z pliku i generowanie rysunków – zarówno rekurencyjnych wykresów IFS złożonych z prostokątów, jak i losowych iteracji złożonych z punktów wg. podanego algorytmu iteracyjnego.

Format plików jest prosty. Pierwsza linia zawiera liczbę odwzorowań i rozmiary prostokąta referencyjnego, natomiast kolejne zawierają opisy odwzorowań w postaci: skala_x skala_y przesunięcie_x przesunięcie_y obrót_w_lewo_w stopniach.

Np. trójkąt sierpińskiego opisany jest w następujący sposób

3 100 100
0.5 0.5 0 0 0
0.5 0.5 25 50 0
0.5 0.5 50 0 0

Zaś nasza choinka tak:

4 200 300
0.9 0.9 10 30 0.0
0.2 0.3 90 -9 85.0
0.2 0.3 108 33 -85.0
0.1 0.3 90 0 0.0


Punktacja:

– wczytywanie IFS z pliku w sposób umożliwiający dalsze przetwarzanie (2 pkt)
– możliwość uruchamiania programu jako skryptu z opcjami z linii komend (-i nazwa pliku -n liczba iteracji -t rodzaj_rysunku) (3 pkt)
– rysowanie wczytanych układów IFS jako prostokątów dla zadanej głębokości rekursji (5 pkt)
– rysowanie wczytanych układów IFS przy pomocy algorytmu losowego dla zadanej liczby punktów (10 pkt).

 Termin:

Zadania nadsyłamy w postaci e-mail’a zawierającego frazę “[WDI-2-2015]” w tytule do prowadzącego ćwiczenia z kopią (CC) do wykładowcy do dnia 17. stycznia 2016 (włącznie). Rozwiązanie powinno być w postaci pojedyńczego pliku .py, zawierającego komentarze wystarczające do uruchomienia programu i oceny rozwiązania, dołączone do e-maila w postaci załącznika (bez kompresji). Tak jak zwykle, ocena jest wpisywana dopiero po zaprezentowaniu rozwiązania prowadzącemu zajęcia, a nie przysłanie programu w terminie powoduje, że tracą państwo 50% punktów