Naszym zadaniem będzie napisanie programu generującego losowe krajobrazy fraktalne.
Losowy krajobraz jest płaszczyzną dwuwymiarową w przestrzeni trójwymiarowej. Zwkle rozważa się płąszczyzny trójkątne lub kwadratowe, my zajmiemy się tym drugim przypadkiem. Płaszczyznę będziemy reprezentować jako macierz wymiaru 2^N+1*2^N+1, gdzie M[i,j] oznacza wysokość (współrzędną Y) punktu o x=i i z=j.
Aby utworzyć losowy krajobraz tego rodzaju, będziemy postępować wg następującego rekurencyjnego schematu:
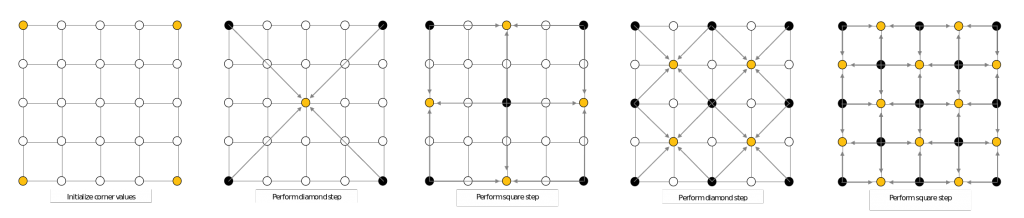
Zacznijmy od zainicjowania wartości narożnych macierzy (krok 0).
Następnie wykonujemy N zejść rekurencyjnych (k przebiega od N do 1):
- (diamond step na schemacie) ustaw wartość każdego punktu środkowego (żółty) na wartość średnią pomiędzy czterema narożnikami (czarnymi)zaburzoną o wartość 2*k*sigma* norm()
- (square step na schemacie) Ustaw wartości czterech wartości na środkach (żółtych) brzegów kwadratu na wartości średnie pomiędzy ich czterema sąsiadami (czarnymi). zaburzoną o ((2 *k)-1)*sigma*norm()
Naszym zadaniem jest nie tylko generowanie takiego krajobrazu, ale także jego wizualizacja w postaci mapy fizycznej (imshow) i płaszczyzny 3D.
Nasz program w wersji podstawowej (10pkt) powinien dać się uruchomić jako skrypt i pozwalać na ustawienie następujących parametrów:
- N – rząd macierzy (2^N+1). Domyślnie 10, powinno działać co najmniej do N=
3014 - sigma – stopień “górzystości” terenu
- map_file – nazwa pliku (pdf lub png) z mapą. Jeśli podane, to mapa jest zapisywana do pliku, jeśli nie, otwieramy okienko z wykresem
- surf_file – nazwa pliku (pdf lub png), z wykresem płaszczyzny. Jeśli podane, to powierzchnia jest zapisywana do pliku, jeśli nie, otwieramy okienko z wykresem
- colormap – mapa kolorów z matplotlib do użycia
- matrix_file – zapis macierzy do pliku
Wersja nieco bardziej zaawansowana (dodatkowe 2 pkt) może obsługiwać także następujące opcje:
- wczytywanie macierzy już częśćiowo wypełnionej i losowanie tylko od kroku K
- Okresowe warunki brzegowe, tak, aby dało się “wykafelkować” większą powierzchnię
Rozwiązania wysyłamy do 3. maja 2016 (włącznie) w postaci e-mail’a do wykładowcy z [ONA-1-2016] w tytule.
Rozwiązania po terminie otrzymują połowę punktów, na które zasługiwałyby w terminie i można je przysyłać do 6 VI 2016).

Zgodnie z Państwa sugestią zmieniłem wymaganie rozmiaru z N=30 do N=14, tak aby na pewno cała macierz mieściła się w pamięci RAM. Warto zastanowić się, jak można byłoby rozwiązać to zadanie gdybyśmy chcieli wygenerować macierz większą niż dostępna pamięć, np. dla N=20. Czy to rzeczywiście byłoby niemożliwe? Jak wyglądałoby rozwiązanie?
We wzorze na zaburzenie pojawia się funkcja norm(), ale bez podania jakiego wektora/macierzy ma to być norma (ta funkcja wymaga jakiegoś argumentu). Czy chodziło o tą funkcję czy może o funkcję normal()?
Chodziło mi o funkcję scipy.stats.norm, ale można też użyć funkcji normal z modułu numpy.random
Jeszcze jedna kwestia, która pojawiła się w dyskusji nad zadaniem:
nieco ładniej będą wyglądać płaszczyzny, które zaburzać będziemy o czynnik
2**k*sigma* norm(), zamiast 2*k*sigma* norm(), tak jak jest w zadaniu. Wiąże się to z wykładniczą zmianą długości odcinków łączących punkty na kolejnych poziomach algorytmu.